题目

https://leetcode.cn/problems/largest-rectangle-in-histogram/description/?envType=featured-list&envId=2cktkvj?envType=featured-list&envId=2cktkvj

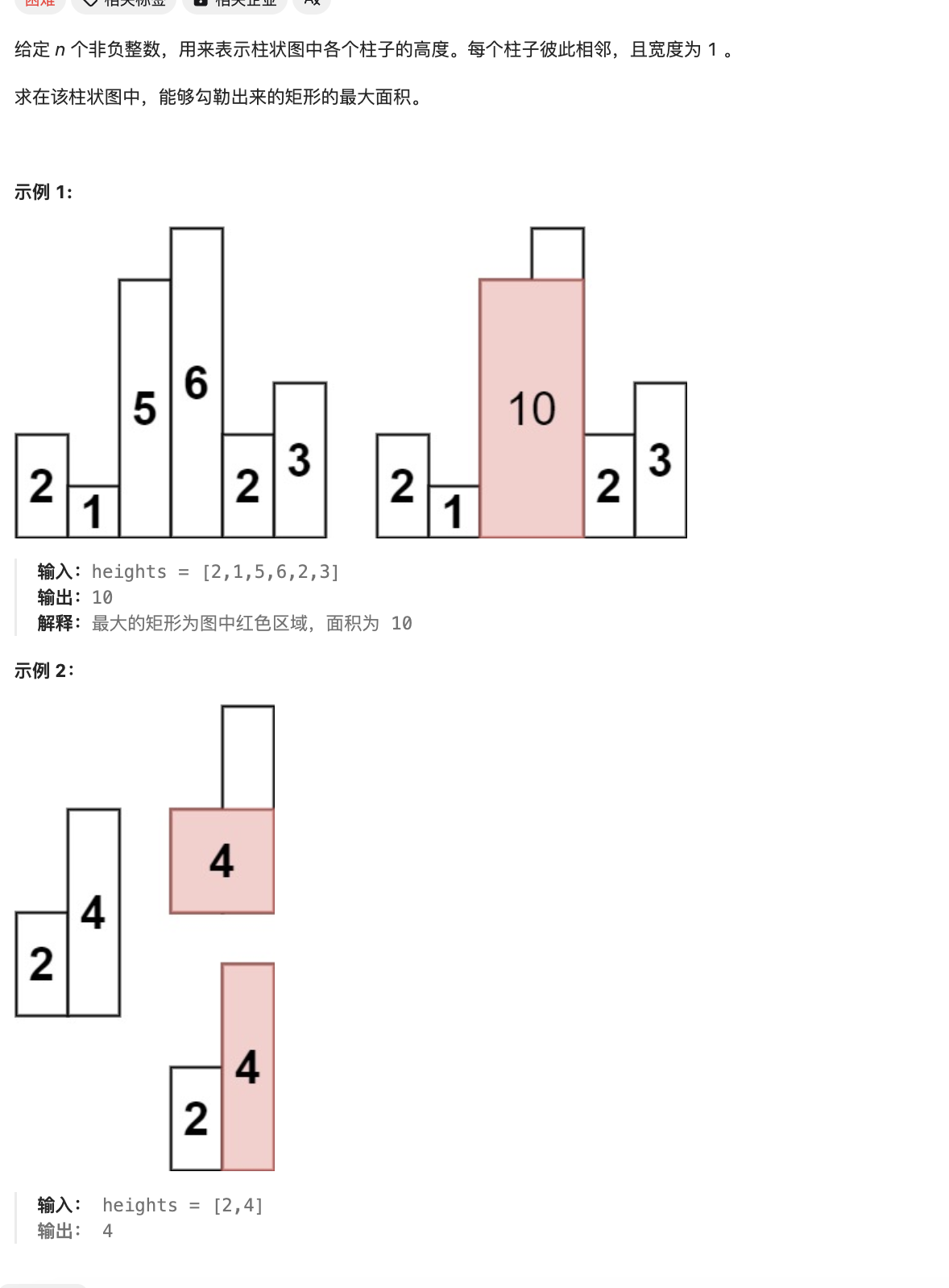
解题

这个应该还是找出隐藏规则的方法

最大面积 左右 连续 有 > 当前的

1. 如果左右 都比 我小 则 面积为 我的高度
2. 如果 左右有比自己高的 则面积为

暴力循环+左右移动

from typing import *


def solution(heights: List[int]):
    length = len(heights)
    max_area = 0
    for i in range(length):
        left = i
        while left > 0 and heights[left - 1] >= heights[i]:
            """
            左边的高度 > 当前高度 可以左移动
            """
            left -= 1
        right = i
        while right < len(heights) - 1 and heights[right + 1] >= heights[i]:
            """
            右边高度
            """
            right += 1
        width = right - left + 1
        max_area = max(max_area, width * heights[i])
    return max_area

这个解法 复杂度应该 在 O(n**2) 在 leetcode 上 会超时

所以应该有其他解法
找到提示应该可以用栈+循环解决

解题思路：

1. 遍历每个柱形的高度，以当前柱形为矩形的高度，向左右两边扩展，直到高度小于当前柱形的高度为止，计算当前矩形的面积，更新最大面积。
2. 为了方便处理边界情况，可以在高度数组的两端各添加一个高度为0的柱形。
3. 使用栈来存储柱形的索引，栈中存储的索引对应的柱形高度是递增的。
4. 遍历高度数组，如果当前柱形的高度大于栈顶柱形的高度，则将当前柱形的索引入栈；否则，弹出栈顶的柱形索引，计算以该索引对应的柱形高度为矩形高度的最大面积，更新最大面积。

from typing import *


def solution(heights: List[int]):
    stack = []
    heights.append(0)  # 在高度数组末尾添加一个高度为0的柱形
    max_area = 0
    for i in range(len(heights)):
        while stack and heights[i] < heights[stack[-1]]:
            """
             1. 当前元素 < 栈道顶部元素(前面一个元素)
             2. 当前元素 > 前面元素 
            """
            h = heights[stack.pop()]
            w = i if not stack else i - stack[-1] - 1
            max_area = max(max_area, h * w)
        # 将元素索引 加入栈
        stack.append(i)
    return max_area